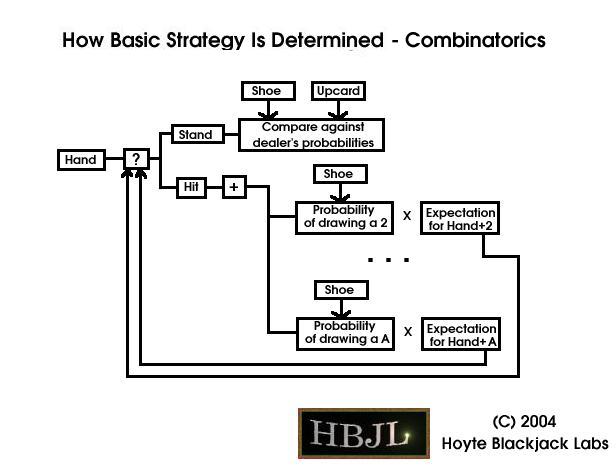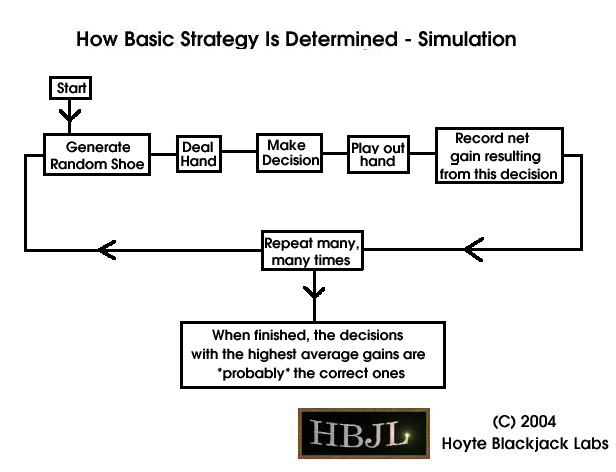
A BS is dependent only on the current hand you posess and the dealer's upcard. By definition, a BS assumes you have no knowledge of the cards that have already been dealt from the shoe. Indeed, this is the reason why a BS is termed "Basic". If a strategy uses information on cards previously dealt, it is no longer a basic strategy.
Since we have no knowledge of the current contents of the shoe, we are forced to assume that the shoe is in its most likely state: a neutral, balanced deck. Because of this reason, a BS is only guaranteed to be perfectly accurate on the very first deal from the shoe (and only then if you are the only one at the table).
For instance, when we examine a specific (common) Blackjack ruleset, we see that when we hold 10,6 vs. 10 we are bound to lose money in the long run no matter what we do. However, when we carefully analyse the situation, we see that if we stand we expect to lose about 57.7 cents for every dollar, but if we hit we will only lose about 57.1 cents for every dollar. Since we lose less, the correct BS decision for this scenario is to hit.
It is important to realize that for any set of Blackjack rules there is one, and only one, correct BS. Some strategies for blackjack are very similar to the BS. These strategies are usually almost indistinguishable from the BS in practice, but it is important to remember that there is only one correct BS for any given set of blackjack rules. Sometimes it is difficult to determine which strategy is the BS and even what we now think is the correct BS could later be reinterpreted more accurately.
In practice, the BS that we use in casinos is a simplified version of the BS that is designed to be easy to memorize and consult. For instance, a hand of 7,9 might have a different BS perscription than 2,2,2,2,3,5 even though the strategy we use in the casinos considers these both to be hard 16s. As such, it perscribes an incorrect play in certain (rare) cases.
One of the most useful aspects of a BS is that it allows us to estimate the player's "advantage" when playing blackjack with a neutral, balanced deck. This is sometimes refered to as the Basic Strategy Expectation (BSE) and is usually expressed in terms of a percentage. It simply corresponds to the average return on investments of your bets. For instance, if the BSE is -0.66%, when you play using the BS, you can expect to lose, in the long run, just over half a cent for every dollar bet. Nearly without exception, the rules offered in casino blackjack games have a negative BSE, giving the advantage to the casino. It is for this reason that casinos don't mind you using the BS to assist your play. In fact, if you ask, many casinos will give you a "player's card" which provides an admirably accurate replication of the BS.
Aside from providing the most effective strategy for casual blackjack playing (where you don't keep track of the cards), BS is frequently used either fully or partially in strategies for keeping track of the cards (called card counting).